T1编辑字符串
不难发现$t$字符串中连续的1,对应着$s$字符串中可以任意调整顺序的一个区间。
那么相当于$s1,s2$有某些区间可以任意调整顺序,问最终能匹配上的最多位数是多少
以下是我的贪心流程:
每一位$i$有4种情况——在$s1,s2$中都可以调;都不可以调;只在某一个字符串中可以调。
不可以调的情况很简单,不多赘述。
如果只在某一个字符串中可以调,假设在$s1$处可以调,相当于$s1[i]$是机动的,我们只需要调动它所在的调整区间中$s2[i]$这个字符到$s1[i]$这里就可以了,所以能匹配上的条件是该区间内还有$s2[i]$这个字符。
如果都可以调,相当于$s1[i],s2[i]$都是机动的,那么任意取0或者1,只要两个字符串这个区间里都还有0或者1这个字符就可以了。
由于$s1[i],s2[i]$都是机动的这个条件很宽松,优先匹配只在某一个字符串里可以调的情况,再处理$s1[i],s2[i]$都是机动的的情况即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
constexpr int MAXN = 1e5;
char s1[MAXN + 5], s2[MAXN + 5];
char t1[MAXN + 5], t2[MAXN + 5];
int Main()
{
int n;
scanf("%d", &n);
scanf("%s%s%s%s", s1 + 1, s2 + 1, t1 + 1, t2 + 1);
std::vector<int> block1(n + 1), block2(n + 1);
std::vector<std::array<int, 2>> sum1(n + 1), sum2(n + 1);
for (int i = 1, cnt = 0; i <= n; ++i)
{
if (t1[i] == '1' && t1[i - 1] == '1')
block1[i] = block1[i - 1];
else if (t1[i] == '1')
block1[i] = ++cnt;
if (t1[i] == '1')
sum1[block1[i]][s1[i] - '0']++;
}
for (int i = 1, cnt = 0; i <= n; ++i)
{
if (t2[i] == '1' && t2[i - 1] == '1')
block2[i] = block2[i - 1];
else if (t2[i] == '1')
block2[i] = ++cnt;
if (t2[i] == '1')
sum2[block2[i]][s2[i] - '0']++;
}
int ans = 0;
for (int i = 1; i <= n; ++i)
{
if (t1[i] == '0' && t2[i] == '1')
{
if (int &cnt = sum2[block2[i]][s1[i] - '0']; cnt > 0)
ans++, cnt--;
}
if (t1[i] == '1' && t2[i] == '0')
{
if (int &cnt = sum1[block1[i]][s2[i] - '0']; cnt > 0)
ans++, cnt--;
}
if (t1[i] == '0' && t2[i] == '0' && s2[i] == s1[i])
ans++;
}
for (int i = 1; i <= n; ++i)
if (t1[i] == '1' && t2[i] == '1')
{
if (std::min(sum2[block2[i]][0], sum1[block1[i]][0]) > 0)
++ans, sum2[block2[i]][0]--, sum1[block1[i]][0]--;
else if (std::min(sum2[block2[i]][1], sum1[block1[i]][1]) > 0)
++ans, sum2[block2[i]][1]--, sum1[block1[i]][1]--;
}
std::cout << ans << "\n";
return 0;
}
int main()
{
freopen("edit.in", "r", stdin);
freopen("edit.out", "w", stdout);
int TestCases = 1;
if constexpr (MultiTestCases == 1)
scanf("%d", &TestCases);
while (TestCases--)
Main();
return 0;
}
|
T2遗失的赋值
设序列是$s$
假设$s_i$由一元关系固定,一个很关键的点是你可以让$a_i\neq s_i$,这样后面你可以随便填(方案是$(v-1)v$。但是如果令$a_i=s_i$,那么$s_{i+1}$就根据你$b_i$的取值而确定,方案是$v$。
如果当前$s_i$和$s_{i+1}$都不知道是多少,相当于上面两种方案都是可行的,因此方案是$v^2$。
推广一下这个结论,两个相邻的$c_j$中间空出来很多$s_i$,相当于两头固定,但中间不确定的一个区间,假设这个区间是$[l,r]$。
那么$a_l$如果等于$s_l$,$s_{l+1}$就固定了,且有$v$种固定它的方案,相当于区间长度缩小了一格,是一个子问题;如果$a_l\neq s_l$,那么,这一位有$(v-1)v$种取值,且后面$[l+1,r-1]$所有的$s_i$都不知道,相当于$a,b$可以随便填;这样我们发现一个区间的方案跟两边的$s_l,s_r$取值无关,跟区间长度(或者说$a_i,b_i$数量)相关。
假设$dp[len]$是区间长为$len+1$(此时有$len$个$a_i,b_i$要填)的方案数。由上一段分析可以得到
$$dp[len]=v*dp[len-1]+(v-1)v*v^{2(len-1)}$$而序列长度$n\leq 10^9$,线性DP可能超时。好在这个方程是$dp[i]$仅和$dp[i-1]$相关,考虑用矩阵加速。
$$\begin{bmatrix}dp[i-1],v(v-1)v^{2(i-1)} \end{bmatrix}
\begin{bmatrix}
v&0\\
1&v^2\\
\end{bmatrix} = \begin{bmatrix}dp[i],v(v-1)v^{2i} \end{bmatrix}$$边界是$dp[1]=(v-1)v + 1$
这样去遍历排好序的$c_j$序列,每次输入一个长度进去将转移矩阵$M$快速幂然后DP即可。
这样可能会超时——因为10组测试数据共用1s,矩阵乘法计算一次需要8次运算。
实际上没必要每次都去算矩阵的快速幂。单次计算一个向量和矩阵的乘法只需要4次操作,不妨预处理$M$的$2^i$次幂,这一步只需要算30次矩阵乘法。
每次求一个长度的$dp$值的时候,直接用$\begin{bmatrix}dp[1],v^3(v-1) \end{bmatrix}$去乘对应的矩阵即可,运算常数减小为4,这个复杂度过题就很充裕了。
另:展开之后可以直接得到公式$dp[i]=v^{2i}-v^{i}+v^{i-1}$,这就可以直接快速幂了…
emm,如果考场上展开比较烦的话用矩阵还是挺好的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
using modint = static_modint<(int)1e9 + 7>;
template <class T, int SIZE = 2>
struct Matrix
{
std::array<std::array<T, SIZE>, SIZE> a{};
Matrix(T v = 0)
{
for (int i = 0; i < SIZE; ++i)
a[i][i] = v;
}
Matrix operator*(const Matrix &rhs) const
{
Matrix res{};
for (int i = 0; i < SIZE; ++i)
for (int j = 0; j < SIZE; ++j)
for (int k = 0; k < SIZE; ++k)
res.a[i][j] += a[i][k] * rhs.a[k][j];
return res;
}
std::array<T, SIZE> &operator[](int i)
{
return a[i];
}
const std::array<T, SIZE> &operator[](int i) const
{
return a[i];
}
};
template <class T>
T quick_pw(T a, ll b)
{
static T I{1};
if (b == 0)
return I;
T ans = I, base = a;
while (b)
{
if (b & 1)
ans = ans * base;
b >>= 1;
base = base * base;
}
return ans;
}
modint DP(int i, int v, const std::array<Matrix<modint>, 30> &trans)
{
i--;
std::array<modint, 2> dp{modint{v - 1} * v + 1, modint{v} * (v - 1) * v * v};
for (int p = 0; p < 30; ++p)
{
if (i >> p & 1)
{
auto pre = dp;
// printf("%d %d\n", pre[0], pre[1]);
dp[0] = pre[0] * trans[p][0][0] + pre[1] * trans[p][1][0];
dp[1] = pre[0] * trans[p][0][1] + pre[1] * trans[p][1][1];
}
}
return dp[0];
}
int Main()
{
int n, m, v;
read(n, m, v);
modint v2 = 1ll * v * v;
std::array<Matrix<modint>, 30> trans{};
trans[0][0][0] = v, trans[0][1][0] = 1;
trans[0][0][1] = 0, trans[0][1][1] = v2;
for (int i = 1; i < 30; ++i)
trans[i] = trans[i - 1] * trans[i - 1];
std::map<int, int> map{};
bool flag = true;
for (int i = 1; i <= m; ++i)
{
int c, d;
read(c, d);
if (map.count(c))
{
if (map[c] != d)
flag = false;
}
map[c] = d;
}
if (!flag)
return printf("0\n"), 0;
int pre = map.begin()->first;
modint ans = v2.pow(pre - 1);
for (auto [c, _] : map)
{
int len = c - pre;
if (len > 0)
ans *= DP(len, v, trans);
pre = c;
}
ans *= v2.pow(n - pre);
printf("%d\n", ans);
return 0;
}
int main()
{
freopen("assign.in", "r", stdin);
freopen("assign.out", "w", stdout);
int TestCases = 1;
if constexpr (MultiTestCases == 1)
scanf("%d", &TestCases);
while (TestCases--)
Main();
return 0;
}
|
T3树的遍历
新树节点度数不超过3。
换句话说:一条边它能扩展它的“兄弟边”(相邻)以及它的儿子边。
假设一条边$(u,v)$,它的父亲有两种可能——$(x,u)$边以及$(u,y)$边。而边$(u,v)$能扩展的边也有两种——$(v,z)$边以及$(u,w)$边。
于是考虑点$(u,v)$能和谁相连——假设它是$u$的儿子边中第$i$个扩展的,那么它可以扩展一个$v$的儿子边,以及$u$的儿子边中剩下一个没扩展的。
它的方案数是$(d_v-1)*(d_u-i-1)$。于是你都乘起来发现答案是$\prod(d_u-1)!$
然后考虑$k=2$的情况。感觉上和这两个边中间的路径有关。
考虑去重的情况。
首先看一下起始边的情况——起始边一定度不超过2。
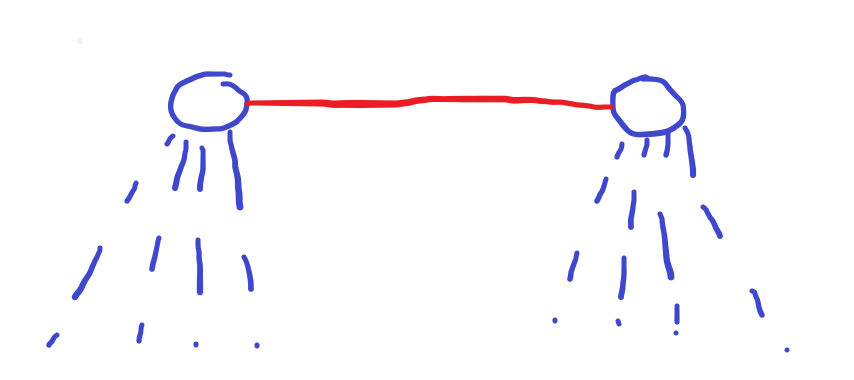
这条红色边作为起始边,只会扩展左右两个虚线边。
所以首先以$(u,v)$为起始边的新树$T1$,如果$(x,y)$在$T1$上的度数为2,则才有可能会重复。
那么$(x,y)$何时度数为2?不妨考虑$(x,y)$的度数何时为3:此时,$(x,y)$会和$x$上两条边相连(其中一条扩展了$(x,y)$,而另一条则被$(x,y)$扩展),和$y$上一条边相连。
所以你如果想让$(x,y)$在$T1$上度为2,那么$(x,y)$不能扩展出$x$的虚线边。等价于$x$的所有边中,这条红色的边是最后扩展的。
于是重复计算了为$(d_x-2)!$次。
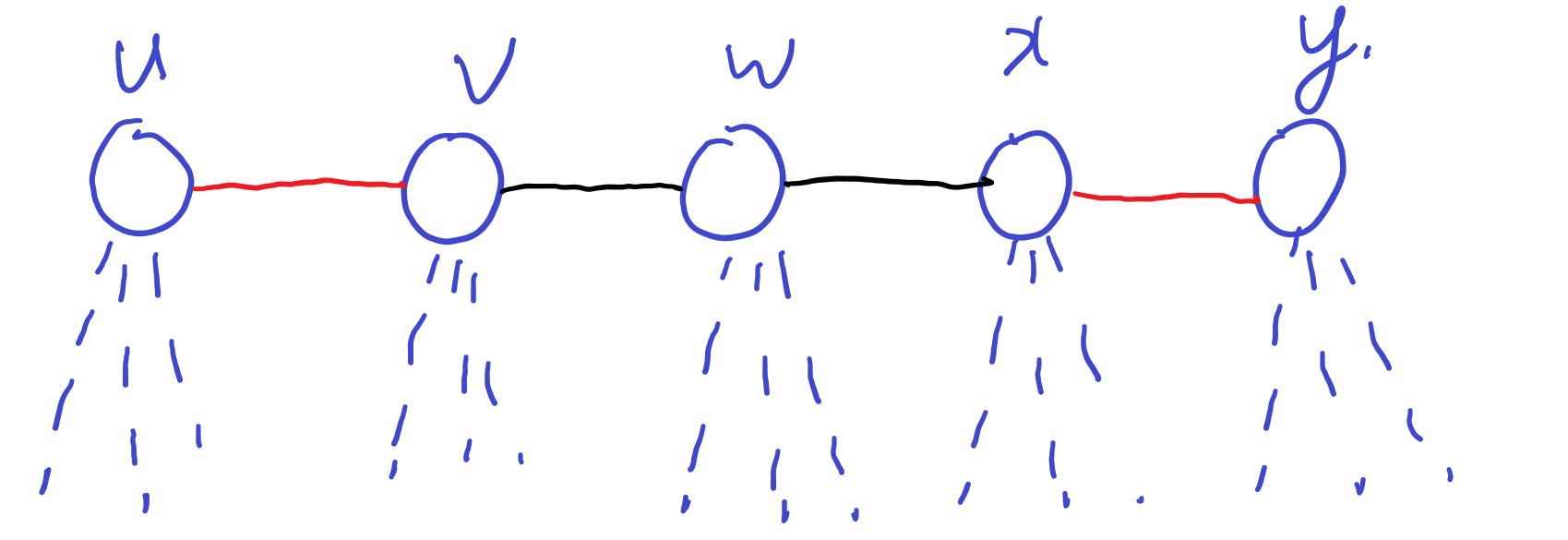
再考虑黑边的情况。以$(w,x)$为例。
这条边在以$(u,v)$为起始边的新树$T1$,它可能连接的有
- $(v,w)$或$w$的一条虚线
- $w$的另一条虚线
- $x$的虚线或$(x,y)$。
这条边在以$(x,y)$为起始边的新树$T2$,它可能连接的有
- $(x,y)$或$x$的一条虚线
- $x$的另一条虚线
- $w$的虚线或$(v,w)$。
如果这条边在新树$T1$中度为3,等于它和$w$中两条线相连,而这种情况在$T2$中不存在;反过来也是一样的,所以发生重复的情况一定也是这条边的度为2。
那么重复计算次数为$(d_w-2)!$
以此类推,最终总的重复数是$(d_v-2)!(d_w-2)!(d_x-2)!$。
更形式化地讲:重复计算了$\prod_{u\in path{e_1,e_2}}(d_u-2)!$。
重复计算?不禁让人想到容斥原理。
所谓重复计算的部分,就是既能以$e_1$为起始边又能以$e_2$为起始边的方案。
要求的是$|e_1 \bigcup e_2|$,等价于$|e_1|+|e_2|-|e_1 \bigcap e_2|$。
进一步推广,对于$k$条边,求的是$|e_1|+…+|e_k|-|e_1\bigcap e_2|-|e_2\bigcap e_3|…+|e_1\bigcap e_2\bigcap e_3|+…$
这样我们化并为交,考虑求能以多条边为起始边的方案。偶数条边交在一起的方案减掉,奇数条边交在一起的方案加起来。
考虑这样一张图:
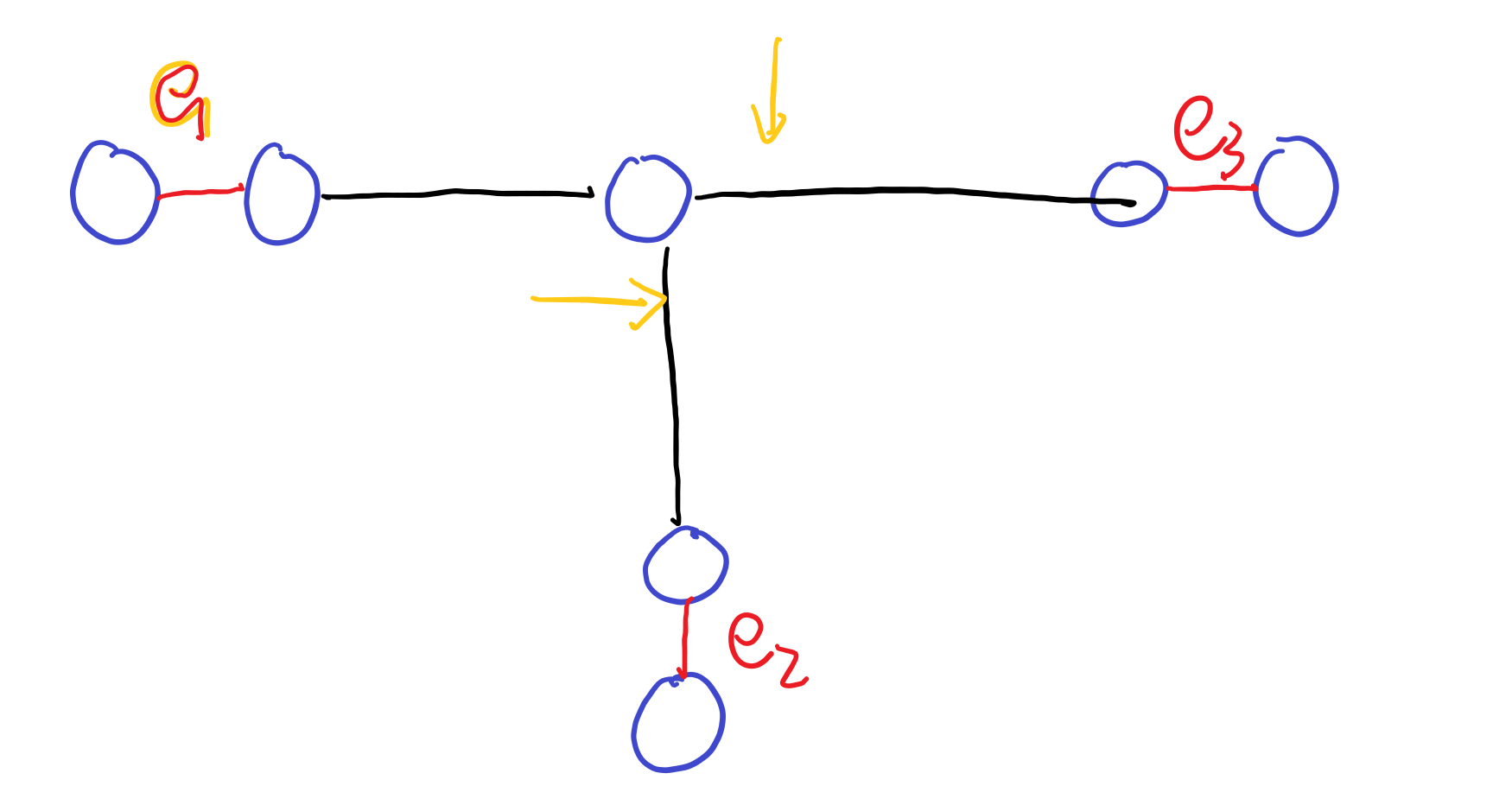
两条黄色箭头指向的边,按上面的分析,分别要求在$e_1->e_3$的新树和$e_1->e_2$的新树中作为中间蓝点的最后一条边来扩展。那么以$e1,e2,e3$为起始边的共同方案在这一个点上出现了矛盾——两条不一样的边都要求是扩展的最后一条边,于是这种分岔的情况,交集的大小是0!
而不分岔的情况,就是所有起始边都在同一条链上,这就方便我们统计了。
写到这里我突然意识到,这种按边扩展的方式有点类似于左儿子右兄弟的树的变换方案。
之前分析过一个点最多度数为3,有一个父亲和两个儿子;令它的左儿子连向它在树上的儿子边,那么右儿子相当于连接的是它的“兄弟边”。于是新树中,一条方向为右的右链对应了原树中从同一个点出发的所有边。

一条右链$(a,b,c,d,e,f)$的大小,正是它们共同邻接点的度数。而由于dfs是从$a$的方向过来的,因此右链的一端固定为$a$;考虑不同的右链形态(或者叫“右链剖分”?),总方案是$\prod(d_u-1)!$
考虑$k=2$的情况实际上是,右链的另一头被固定了,所以右链形态变成了$(d_u-2)!$
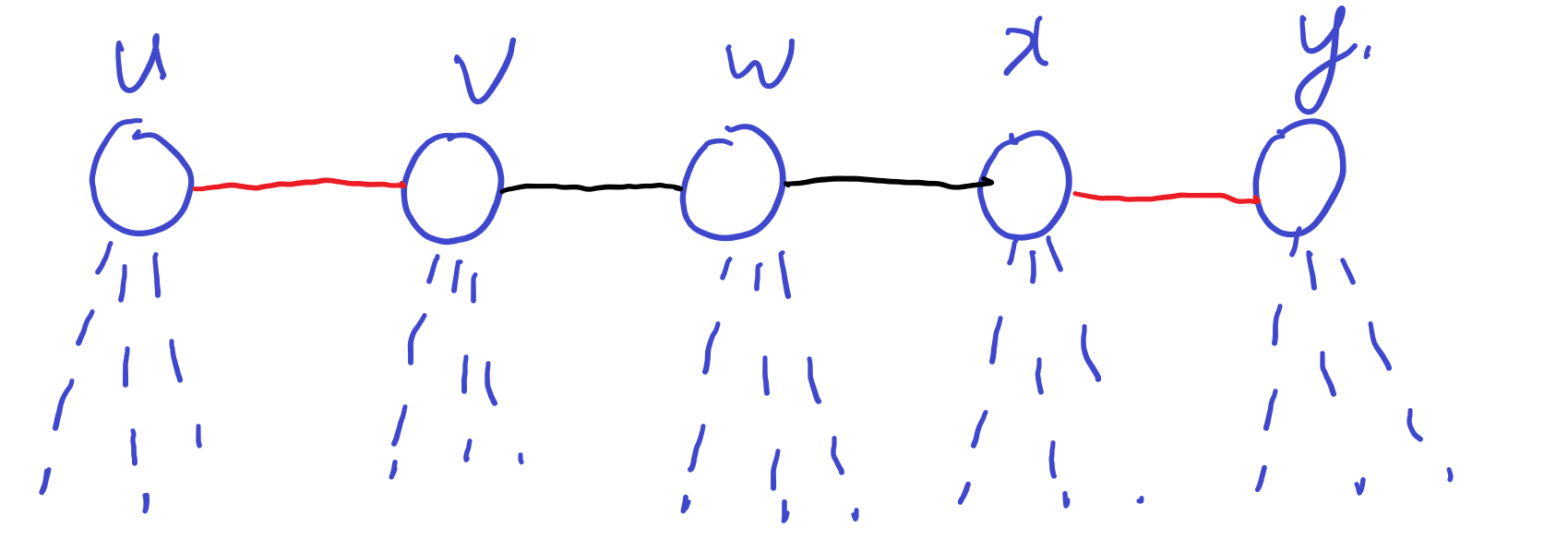
这张图上,$v$的虚边是右链上能随便移动的,刨去红边和黑边一共有$d_v-2$条边在右链上形态随意。
所以为什么分岔的时候交集为0?因为你规定了两个右链的链尾,显然矛盾。
所以我们最终要计数的是:一条以关键边为两端的路径$p$,权值为$\prod_{u\in p}\frac{1}{d_u-1}$(因为总方案是$\prod(d_u-1)!$,在这条路径上的点要变成$(d_u-2)!$,相当于除以一个$(d_u-1)$)。这条路径上除去两端仍有$q$条关键边,这些边可选可不选,每一种选法这条路径的权值都被重算一遍。
注意到我们要做的是容斥。如果一种选法选了$x$关键边,如果$x$是偶数,由容斥系数是-1;反之容斥系数是1。那么我们只需要关注这条路径$p$上选奇数个边和偶数个边的选法,再乘上路径权重就可以。
注意到我们统计的东西是一条路径的权值和路径上边的选法。对于树上路径的统计问题,有很多种做法,由于这里有求和,因此考虑直接树上DP。
设$dp[u][0]、dp[u][1]$分别表示$u$子树向父亲方向选了偶数/奇数条路径的权值*选法之和。
有$dp[u][0]=\frac{1}{d_u-1}\sum_{v\in son(u)} dp[v][0], dp[u][1]=\frac{1}{d_u-1}\sum_{v\in son(u)} dp[v][1]$
另外:如果$u,v$是关键边,则加上这条边,让$\frac{1}{d_u-1}(dp[v][0]+1)$也转移到$dp[u][1]$里,$\frac{1}{d_u-1}dp[v][1]$也转移到$dp[u][0]$里。并且要注意在$u,v$处结算一条向下的路径,贡献加到$ans$里。
然后在$u$处合并两个儿子的答案作为一条整路径的贡献加到$ans$里。
具体实现看代码。
实际上有一个特别有意思的是:假设一条以关键边为两端的路径$p$,除去两端,路径上还有$q$个关键边,这条路径的点权积为$F$。
看看这个$F$怎么向答案做贡献。
枚举选择关键边的数量$i$,方案是$C_q^iF$,容斥系数为$(-1)^{i-1}$。所以贡献总数是$\sum_{i=0}^q (-1)^{i-1}C_q^iF$。
把这个式子乘一个$-1$进去,发现是$\sum_{i=0}^q (-1)^{i}C_q^iF=F(1+(-1))^q=0$。
所以实际上能为答案做贡献的,只有以关键边为两端,且中间再无其它关键边的路径,找这样的路径做统计就行(点分治、树上DP都可以做)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
using modint = static_modint<(int)1e9 + 7>;
constexpr int MAXN = 1e5;
int d[MAXN + 5];
std::vector<std::pair<int, int>> adj[MAXN + 5];
std::array<modint, 2> dp[MAXN + 5];
int key[MAXN + 5];
modint fac[MAXN + 5], invfac[MAXN + 5], inv[MAXN + 5];
modint ans = 0;
void init(int n)
{
std::fill(d + 1, d + n + 1, 0);
std::fill(key + 1, key + n + 1, 0);
std::fill(adj + 1, adj + n + 1, std::vector<std::pair<int, int>>{});
std::fill(dp + 1, dp + n + 1, std::array<modint, 2>{});
fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = fac[i - 1] * i;
invfac[n] = fac[n].inv();
for (int i = n - 1; i >= 1; --i)
invfac[i] = invfac[i + 1] * (i + 1), inv[i + 1] = fac[i] * invfac[i + 1];
inv[1] = 1;
ans = 0;
}
void dfs(int u, int fa)
{
std::vector knakpack(2, std::array<modint, 2>{});
for (auto [v, i] : adj[u])
{
if (v == fa)
continue;
dfs(v, u);
std::array<modint, 2> f{};
f[0] = dp[v][0] * inv[d[u] - 1];
f[1] = dp[v][1] * inv[d[u] - 1];
if (key[i])
{
ans -= dp[v][1], ans += dp[v][0];
f[0] += dp[v][1] * inv[d[u] - 1];
f[1] += dp[v][0] * inv[d[u] - 1] + inv[d[u] - 1];
}
dp[u][0] += f[0], dp[u][1] += f[1];
ans -= knakpack[0][0] * f[0] + knakpack[0][1] * f[1];
ans += knakpack[0][1] * f[0] + knakpack[0][0] * f[1];
knakpack[1][0] = knakpack[0][0] + dp[v][0] + key[i] * dp[v][1];
knakpack[1][1] = knakpack[0][1] + dp[v][1] + key[i] * (dp[v][0] + 1);
std::swap(knakpack[0], knakpack[1]);
}
}
int Main()
{
int n, k;
read(n, k);
init(n);
for (int i = 1; i < n; ++i)
{
int u, v;
read(u, v);
adj[u].push_back({v, i}), adj[v].push_back({u, i});
d[u]++, d[v]++;
}
for (int i = 1; i <= k; ++i)
{
int e;
read(e);
key[e] = 1;
}
dfs(1, 0);
modint p = 1;
for (int i = 1; i <= n; ++i)
p *= fac[d[i] - 1];
ans *= p;
ans += p * k;
printf("%d\n", ans);
return 0;
}
int main()
{
int c, TestCases = 1;
if constexpr (MultiTestCases == 1)
scanf("%d%d", &c, &TestCases);
while (TestCases--)
Main();
return 0;
}
|
T4树上查询
首先LCA具有一个优美的性质:
$LCA([l,r])$是$a[i]=LCA(i,i+1)$中,$[l,r-1]$内深度最小的那个点。
可以这样理解:
$LCA([l,i-1])$和$i$的lca是$LCA([l,i])$。如果$LCA([l,i-1])\neq LCA([l,i])$, $LCA([l,i])$一定是$i$和$[l,i-1]$其中某一个点的lca(其实都相同)。就让它等于$lca(i-1,i)$。
所以当区间LCA发生变化的时候,一定是$i-1,i$的LCA跟之前的不一样,且变化成$i-1,i$的LCA。
因此求出相邻两点的LCA放在$a[i]$里,在$[l,r-1]$上取最小即可。
接下来发现查询是一个滑动窗口。
根据CF212D的套路,可以用单调栈处理以$a[i]$为最小值的区间,假设它为$x[i],y[i]$。
那么$a[i]$可以更新左端点在$[x[i],i]$,右端点在$[i, y[i]]$的滑动窗口的答案。
这中间有一个$i$很讨厌,考虑放宽限制,如果窗口全落在$[x[i],i]$里,它的答案一定$\geq a[i]$。因为根据单调栈的结论,这个区间的最小值比$a[i]$大。全落在右边是同样的结论。
因此一个窗口只要落在$[x[i],y[i]]$里,答案就$\geq a[i]$
一个询问是在区间$[l,r]$里滑一个长为$k$的窗口,考虑它的答案是否能$\geq a[i]$。那么在这里滑的窗口,需要落在$[x[i],y[i]]$里。
等价于区间$[l,r]$和$[x[i],y[i]]$的交大于等于$k$。
考虑交起来的情况:
- $x[i] \leq l$,此时合法的区间为$y[i]\geq l+k-1$ 扫描线处理$x[i]\leq l$,在线段树上单点修改$y[i]$;然后查询$[l+k-1, n]$的最大值。
- $x[i] \geq l$, 此时合法的区间是$y[i]-x[i]+1\geq k$且$r-x[i]+1\geq k$。这一部分把区间和询问挂在“长度”上,倒序扫描长度,在$x[i]$处单点修改,在$[l, r-k+1]$查询最大值。
两遍扫描线即可更新所有答案。
复杂度$O(nlog_2n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
|
constexpr int MAXN = 5e5;
std::vector<int> adj[MAXN + 5];
int fa[20][MAXN + 5], dep[MAXN + 5];
int st[20][MAXN + 5];
int a[MAXN + 5];
int lca(int u, int v)
{
if (dep[u] < dep[v])
std::swap(u, v);
const int lg = 19;
for (int i = lg; i >= 0; --i)
if (dep[fa[i][u]] >= dep[v])
u = fa[i][u];
if (u == v)
return u;
for (int i = lg; i >= 0; --i)
if (fa[i][u] != fa[i][v])
u = fa[i][u], v = fa[i][v];
return fa[0][u];
}
void dfs(int u)
{
for (int p = 1; (1 << p) <= dep[u]; ++p)
fa[p][u] = fa[p - 1][fa[p - 1][u]];
for (int v : adj[u])
{
if (v == fa[0][u])
continue;
dep[v] = dep[u] + 1;
fa[0][v] = u;
dfs(v);
}
}
int rmq(int l, int r)
{
int p = std::log2(r - l + 1);
return std::max(st[p][l], st[p][r - (1 << p) + 1]);
}
struct Segment
{
int l, r, w;
};
Segment s[MAXN + 5];
struct Point
{
int p, w;
};
int ans[MAXN + 5];
struct Query
{
int l, r, k;
};
Query qry[MAXN + 5];
template <typename Info, typename Merge = std::plus<Info>>
struct SegmentTree
{
const int n;
const Merge merge;
struct node
{
Info info;
};
std::vector<node> tree;
SegmentTree(int _n) : n(_n), merge(Merge()), tree(_n * 4 + 5)
{
}
SegmentTree(std::vector<Info> &init, int _n) : SegmentTree(_n)
{
std::function<void(int, int, int)> build = [&](int p, int l, int r)
{
if (l == r)
{
tree[p].info = init[l];
return;
}
int mid = (l + r) / 2;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
pull(p);
};
build(1, 1, n);
}
void pull(int p)
{
tree[p].info = merge(tree[p << 1].info, tree[p << 1 | 1].info);
}
void modify(int p, int l, int r, int x, const Info &v)
{
if (l == r)
return tree[p].info = merge(tree[p].info, v), void();
int mid = (l + r) >> 1;
if (x <= mid)
modify(p << 1, l, mid, x, v);
else
modify(p << 1 | 1, mid + 1, r, x, v);
pull(p);
}
void modify(int p, const Info &v)
{
modify(1, 1, n, p, v);
}
Info query(int p, int l, int r, int x, int y)
{
if (l == x && r == y)
return tree[p].info;
int mid = (l + r) >> 1;
if (y <= mid)
return query(p << 1, l, mid, x, y);
else if (x > mid)
return query(p << 1 | 1, mid + 1, r, x, y);
else
return merge(query(p << 1, l, mid, x, mid), query(p << 1 | 1, mid + 1, r, mid + 1, y));
}
Info query(int l, int r)
{
return query(1, 1, n, l, r);
}
};
struct Merge
{
int operator()(int a, int b) const
{
return std::max(a, b);
}
};
void solve1(int n, int q)
{
std::vector<std::vector<std::array<int, 3>>> ask(n + 1);
// for (int i = qry[2].l; i <= qry[2].r - 1; ++i)
// printf("%d%c", a[i], " \n"[i == qry[2].r - 1]);
for (int i = 1; i <= q; ++i)
{
auto [l, r, k] = qry[i];
if (k == 1)
ans[i] = rmq(l, r);
else
{
k--;
ask[l].push_back({l + k - 1, n, i});
}
}
std::vector<std::vector<std::array<int, 2>>> events(n + 1);
for (int i = 1; i <= n; ++i)
{
auto [l, r, w] = s[i];
events[l].push_back({r, w});
}
SegmentTree<int, Merge> segment_tree(n);
for (int i = 1; i <= n; ++i)
{
for (auto [r, w] : events[i])
segment_tree.modify(r, w);
for (auto [l, r, id] : ask[i])
ans[id] = std::max(ans[id], segment_tree.query(l, r));
}
}
void solve2(int n, int q)
{
std::vector<std::vector<std::array<int, 3>>> ask(n + 1);
for (int i = 1; i <= q; ++i)
{
auto [l, r, k] = qry[i];
k--;
ask[k].push_back({l, r - k, i});
}
std::vector<std::vector<std::array<int, 2>>> events(n + 1);
for (int i = 1; i <= n; ++i)
{
auto [l, r, w] = s[i];
events[r - l + 1].push_back({l, w});
}
SegmentTree<int, Merge> segment_tree(n);
for (int i = n; i >= 1; --i)
{
for (auto [l, w] : events[i])
segment_tree.modify(l, w);
for (auto [l, r, id] : ask[i])
ans[id] = std::max(ans[id], segment_tree.query(l, r));
}
}
int Main()
{
int n;
read(n);
for (int i = 1; i < n; ++i)
{
int u, v;
read(u, v);
adj[u].push_back(v), adj[v].push_back(u);
}
dep[1] = 1;
dfs(1);
for (int i = 1; i <= n - 1; ++i)
a[i] = dep[lca(i, i + 1)];
for (int i = 1; i <= n; ++i)
st[0][i] = dep[i];
for (int p = 1; p <= 19; ++p)
for (int i = 1; i + (1 << p) - 1 <= n; ++i)
{
int j = i + (1 << (p - 1));
st[p][i] = std::max(st[p - 1][i], st[p - 1][j]);
}
std::stack<int> stack{};
std::vector<std::pair<int, int>> d(n + 1);
for (int i = 1; i <= n - 1; ++i)
{
while (stack.size() && a[stack.top()] >= a[i])
{
s[stack.top()].r = i - 1;
stack.pop();
}
if (stack.size())
s[i].l = stack.top() + 1;
else
s[i].l = 1;
stack.push(i);
}
while (stack.size())
s[stack.top()].r = n - 1, stack.pop();
for (int i = 1; i <= n - 1; ++i)
s[i].w = a[i];
// for (int i = 1; i <= n - 1; ++i)
//{
// printf("%d %d %d\n", s[i].l, s[i].r, s[i].w);
// }
int q;
read(q);
for (int i = 1; i <= q; ++i)
read(qry[i].l, qry[i].r, qry[i].k);
solve1(n - 1, q);
solve2(n - 1, q);
for (int i = 1; i <= q; ++i)
printf("%d\n", ans[i]);
return 0;
}
int main()
{
int TestCases = 1;
if constexpr (MultiTestCases == 1)
scanf("%d", &TestCases);
while (TestCases--)
Main();
return 0;
}
|




