CF2026A
题目链接
题意
在一个第一象限$X\times Y$的方格里,输出两条长度不小于$K$,且垂直的线段。数据保证有解。
解法
直接模拟,从原点开始找长度不超过$K$的线段,判定它垂直方向上在不在方格里
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
int Main()
{
int X, Y, K;
read(X, Y, K);
for (int x = 0; x <= X; ++x)
{
int y = sqrtl(K * K - x * x);
while (y * y < K * K - x * x)
y++;
if (y > Y || y > x)
continue;
printf("0 0 %d %d\n", x, y);
printf("0 %d %d 0\n", x, y);
break;
}
return 0;
}
|
CF2026B
题目链接
题意
有无穷大个白格子,其中有$n$个需要染色。你需要决定一个数值$k$,每次操作选择两个白格子$i$和$j$,且$|i-j|\leq k$来染色。除了$n$个必须染色的格子外,最多可以多染1个。请问你决定的数值$k$最小是多少。
解法
不难发现当$n$是偶数的时候,这个值就是相邻两个必染格子的最大差值。
当$n$是奇数的时候,会有一个格子和多出来的染色格子一起染色。枚举这个格子,回到$n$是偶数的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
int Main()
{
int n;
read(n);
std::vector<ll> a(n + 1);
for (int i = 1; i <= n; ++i)
read(a[i]);
if (n % 2 == 0)
{
ll mx = 1;
for (int i = 1; i <= n; i += 2)
mx = std::max(a[i + 1] - a[i], mx);
std::cout << mx << std::endl;
return 0;
}
ll ans = std::numeric_limits<ll>::max();
for (int i = 1; i <= n; ++i)
{
ll mx = 1;
for (int j = 1; j <= n; j += 2)
{
if (j == i)
j++;
if (j > n)
break;
int nxt = j + 1;
if (nxt == i)
nxt++;
mx = std::max(a[nxt] - a[j], mx);
}
ans = std::min(ans, mx);
}
std::cout << ans << std::endl;
return 0;
}
|
CF2026C
题目链接
题意
你去买东西,第$i$天的商品花费$i$元。但是你能去商店的日子是有限的,用一个01串来表示。
买超过两件商品有折扣,最贵的那件就不用付钱了。
你想把每件商品买且仅买一件。问最少花多少钱。
解法
因为最少花的钱等价于所有商品价值减去我省下的钱,因此考虑如何省更多钱。
如果第$i$天能去商店,显然买两件以上商品,最多能省$i$元。不妨从后向前贪心。
第$i$天如果能去商店,且能买两件商品,那么$i$天之前的商品与之前为了打折多买的前i天商品的差不小于2。
维护这个多买的商品值。如果能买2件以上,则这个值增加1。如果$s[i]=0$,则这个值减1——因为相当于可以用这一天的商品抵消掉之前多买的,剩余多买的商品数少1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
int Main()
{
int n;
std::cin >> n;
std::string s;
std::cin >> s;
int bought = 0;
ll mx = 0;
for (int i = n; i >= 1; --i)
{
if (s[i - 1] == '0')
{
// bought = 0;
if (bought > 0)
bought--;
}
if (s[i - 1] == '1')
{
if (i - bought >= 2)
{
mx += i;
bought++;
}
}
}
std::cout << 1ll * n * (n + 1) / 2 - mx << std::endl;
return 0;
}
|
CF2026D
题目链接
题意
把$a$数组所有区间按左端点为第一关键字,右端点为第二关键字排序,得到新的数组$b$,数组的第$i$个元素是排名为$i$的区间的区间和。
现有$q$个询问,每次询问给出一个$l,r$,询问$b$数组的$[l,r]$区间和。
解法
前缀和套前缀和的套娃题。
首先$b$数组可以写成一个二维表的形式。
第$i$行,$n-i+1$个元素,表示左端点为$i$的区间和。
当给出一个$l$的时候,可以等差数列+二分确定它在哪一行哪一列。对$r$是同理的。
这样发现一个查询分为两种情况。
-
$l$和$r$在同一行$i$;这种情况对应着左端点$i$相同、右端点连续的区间和。相当于$\sum_{j=i+l}^{i+r}(sum[j]-sum[i])$,展开发现是前缀和的一段区间和减去$sum[i]$的一个倍数。那么预处理前缀和的前缀和就行了。
-
$l$和$r$不在同一行。这对应着在$l$那一行的一段后缀和、在$r$那一行的一段前缀和、中间几行是满的;前两部分可以和上一种情况用同样的手法处理,中间满的几行可以预处理行$i$取满的值$row[i]=\sum_{j=i}^n (sum[j]-sum[i])$,显然还是前缀和的前缀和处理一下,并且再求一个$row[i]$的前缀和。
这样就全部解决了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
int Main()
{
int n;
read(n);
std::vector<int> a(n + 1);
std::vector<ll> sum(n + 1);
for (int i = 1; i <= n; ++i)
read(a[i]);
for (int i = 1; i <= n; ++i)
sum[i] = sum[i - 1] + a[i];
std::vector<ll> sum2(n + 1);
for (int i = 1; i <= n; ++i)
sum2[i] = sum2[i - 1] + sum[i];
std::vector<ll> row(n + 1);
for (int i = 1; i <= n; ++i)
row[i] = sum2[n] - sum2[i - 1] - 1ll * (n - i + 1) * sum[i - 1];
std::vector<ll> sumr(n + 1);
for (int i = 1; i <= n; ++i)
sumr[i] = sumr[i - 1] + row[i];
int q;
read(q);
auto find = [&](ll x) -> std::pair<int, int>
{
int l = 1, r = n;
while (l <= r)
{
int mid = (l + r) >> 1;
if (1ll * mid * (n + n - mid + 1) / 2 >= x)
r = mid - 1;
else
l = mid + 1;
}
// printf("find(%lld) = ", x);
x -= 1ll * (l - 1) * (n + n - l + 2) / 2;
// printf("%lld %lld\n", l, x);
return {l, x};
};
while (q--)
{
ll l, r;
read(l, r);
auto [r1, c1] = find(l);
auto [r2, c2] = find(r);
if (r1 == r2)
{
ll res = sum2[r1 - 1 + c2] - sum2[r1 - 1 + c1 - 1] - 1ll * (c2 - c1 + 1) * sum[r1 - 1];
printf("%lld\n", res);
}
else
{
ll res = 0;
if (r1 + 1 <= r2 - 1)
res += sumr[r2 - 1] - sumr[r1];
res += sum2[n] - sum2[c1 - 2 + r1] - 1ll * (n - (r1 + c1 - 1) + 1) * sum[r1 - 1];
res += sum2[c2 + r2 - 1] - sum2[r2 - 1] - 1ll * c2 * sum[r2 - 1];
printf("%lld\n", res);
}
}
return 0;
}
|
CF2026E
题目链接
题意
有$n$个数$a[i]$,选择一个子序列使得子序列的长度减去子序列的或和的$popcount$最大。
解法
实际上换一种说法就是——如果取$a[i]$,得到1的收益,并且损失$popcount(a[i])$;同一位下的损失只计算一次。
那么这实际上就是最大权闭合子图——把$a[i]$为1的位拿出来,把$i$向二进制上为1的位连边,$i$是正权,二进制位是负权,取了$a[i]$就得选这些为1的位。
实际上构图出来是个二分图,算一下最小割,然后用正权和减一下即可。
如果这个题每个数、每个位都带一个权重可能模型会更直白一点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
|
struct Flow
{
static constexpr int INF = 1e9;
int n;
struct Edge
{
int dest, cap;
Edge(int dest, int cap) : dest(dest), cap(cap) {}
};
std::vector<Edge> e;
std::vector<std::vector<int>> g;
std::vector<int> cur, h;
Flow(int n) : n(n), g(n) {}
bool bfs(int s, int t)
{
h.assign(n, -1);
std::queue<int> que;
h[s] = 0;
que.push(s);
while (!que.empty())
{
int u = que.front();
que.pop();
for (int i : g[u])
{
auto [v, c] = e[i];
if (c > 0 && h[v] == -1)
{
h[v] = h[u] + 1;
if (v == t)
return true;
que.push(v);
}
}
}
return false;
}
int dfs(int u, int t, int f)
{
if (u == t)
return f;
int r = f;
for (int &i = cur[u]; i < int(g[u].size()); ++i)
{
int j = g[u][i];
auto [v, c] = e[j];
if (c > 0 && h[v] == h[u] + 1)
{
int a = dfs(v, t, std::min(r, c));
e[j].cap -= a;
e[j ^ 1].cap += a;
r -= a;
if (r == 0)
return f;
}
}
return f - r;
}
void addEdge(int u, int v, int c)
{
g[u].push_back(e.size());
e.emplace_back(v, c);
g[v].push_back(e.size());
e.emplace_back(u, 0);
}
ll flow(int s, int t)
{
ll ans = 0;
while (bfs(s, t))
{
cur.assign(n, 0);
ans += dfs(s, t, INF);
}
return ans;
}
};
int Main()
{
int n;
read(n);
std::vector<ll> a(n + 1);
for (int i = 1; i <= n; ++i)
read(a[i]);
Flow graph(n + 60 + 2);
int S = 0, T = n + 60 + 1;
for (int p = 1; p <= 60; ++p)
{
for (int i = 1; i <= n; ++i)
{
if (a[i] & (1ll << (p - 1)))
graph.addEdge(i, p + n, Flow::INF);
}
graph.addEdge(n + p, T, 1);
}
for (int i = 1; i <= n; ++i)
graph.addEdge(S, i, 1);
int cut = graph.flow(S, T);
// printf("%d\n", cut);
std::cout << n - cut << std::endl;
return 0;
}
|
CF2026F
题目链接
题意
一开始有一个1号商店,接下来有$q$个操作。
$1\ x$表示新开一个商店并复制$x$商店
$2\ x\ p\ t$表示在商店$x$里加入一个容量为$p$,价值为$t$的商品
$3\ x$把商店$x$最早加入的商品去除
$4\ x\ p$询问在商店$x$花费$p$元钱最多能买多少价值的商品
解法
如果没有1操作,就是在一个队列上一边push元素一边pop元素,询问是在队头和队尾中间做01背包。
有1操作的情况下,就是在可持久化队列里做01背包。
由于没有强制在线可以考虑离线。
在真正解决这个问题之前,先考虑三个前置问题。
在栈上做背包
在栈上push一个元素,或者pop掉栈顶,并维护背包的DP值。
由于背包的DP,$dp[i][j]$从$dp[i-1][j]$和$dp[i-1][j-v[i]]$转移过来。
那么正常做背包的过程就相当于不断push一个元素,更新dp数组。
当pop掉栈顶的时候,等价于最后一个元素被移除了,这时我们让$n$(代表物品数量)直接变回$n-1$,取$dp[n-1]$的DP值就好。
在队列上做背包
相比在栈上做背包,在队列上做背包的难点是移除了最开头的元素。
如果移除的是末尾的元素,那么非常好做。
为了解决这个问题,可以想象目前在队头和队尾中间有一条线。
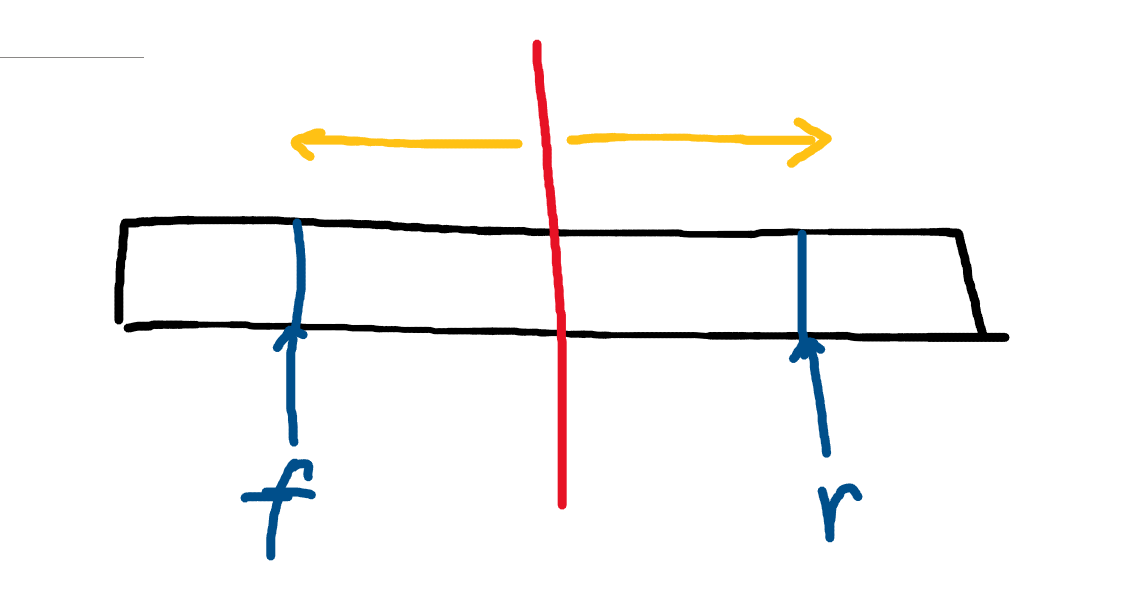
考虑维护左右两个dp数组,分别叫$dpl$和$dpr$。
$dpr$从红线向队尾按正向推,$dpl$从红线向队头按逆向推。
这样队列pop元素的时候,相当于从$dpl$移除末尾的一层,就很好做了。
如果$dpl$空了,就考虑重新画线在队尾处,将$dpl$重新算一遍并且清空$dpr$。
这样看起来复杂度好像很高。但是考虑一个物品会在哪里做DP。
一个物品会在正向的$dpr$数组里通过push操作做一层DP,并且重构$dpl$的时候会在逆向的$dpl$数组里做一层DP。于是总的DP层数不超过$2n$。
在回答一个询问的时候,合并$dpl$和$dpr$两个数组。具体来说就是枚举左右的体积$i$和$V-i$,加起来求最大值即可。
于是复杂度是$O(nV+qV)$
在双端队列上做背包
这个问题相比上一个问题,在队头和队尾处都会增加、删除元素。
不过与普通队列相比,增删元素都是在对应的dp数组末尾增加或移除一层,复杂度是不变的。
问题在于重构操作。假设依旧是某一边空了,直接重构,将另一边清空的情况。
可能会出现左空,pop左,全部重构到左边;然后pop右,全部重构到右边;接下来再次pop左,全部重构到左边…这样左右横跳的操作。
假设重构并不清空一边,而是重画一条线,考虑这条线画在哪里。一般来说为了避免上述情况会画在队头和队尾的中间。这样做的时间复杂度是怎样的呢?
以下是我个人比较民科的思考:
假设当前队列有$x$个元素,那么重构一次左右两边分别有$\frac{x}{2}$个元素。
距离下一次重构可能发生的事情是,某一边空了,另一边被塞了$k$个数。
于是在某一边净pop一共$\frac{x}{2}$次,对这一边的总操作次数必然大于等于它;在另一边净push一共$k$次,对这一边总操作次数也必然大于等于它。
那么下一次重构操作一共做了$O(k+\frac{x}{2})$层DP。
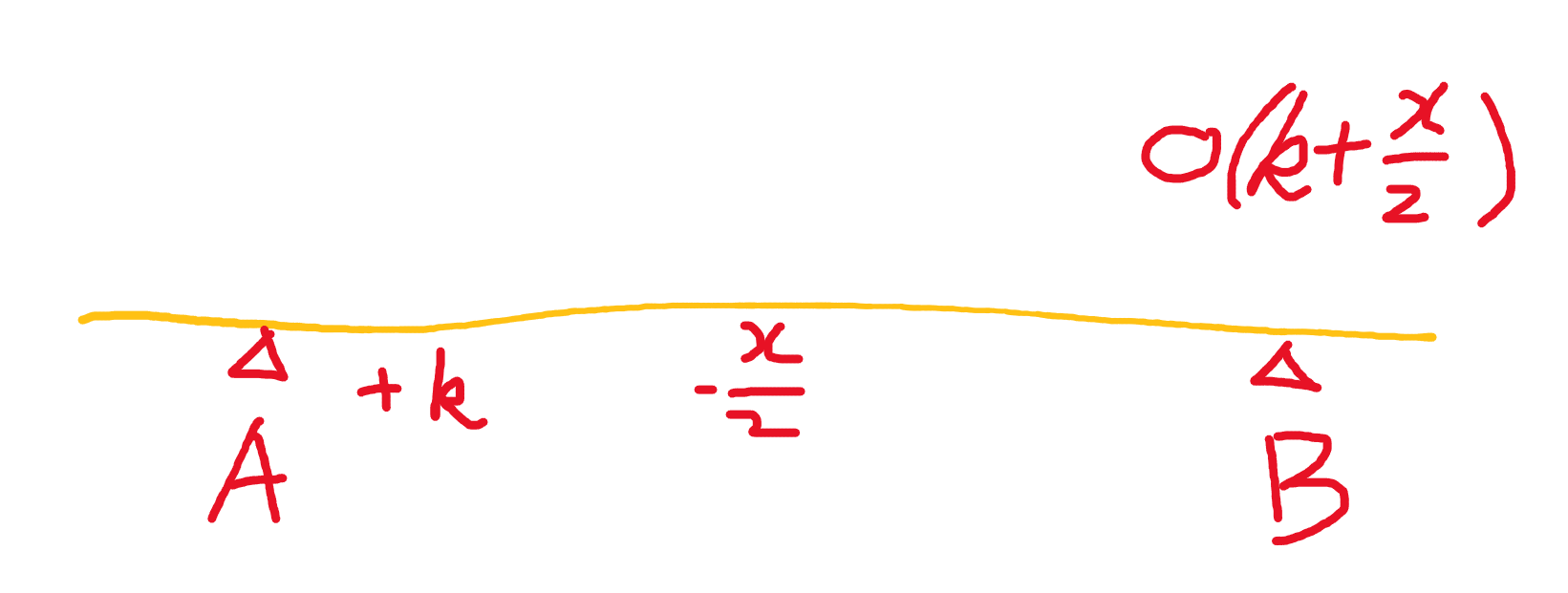
于是我们发现这两次重构操作之间的操作数$\geq k+\frac{x}{2}$。那么一次重构操作的DP层数,小于等于它和上一次重构操作之间的距离,相当于一个差分!
那么重构的总DP层数,等价于最后一次重构到一开始之间的操作数,不会超过总操作数$n$。
所以在双端队列这样重构的复杂度是$O(nV)$的。$n$是总操作数。
至于其它操作和普通队列复杂度是等价的。
因此最终复杂度依然是$O(nV+qV)$
本题的解法
把所有操作离线,按NOIP2023三值逻辑的拆点方案,做一棵版本树。
每一次复制、增加、删除操作都是新增一个节点,并接在原节点上。把具体的操作参数写在父亲向儿子的边上。
询问操作就挂在对应版本对应的节点上。
这样自顶向下DFS的过程,相当于从后push、从前pop的队列背包。
而DFS的回溯过程,相当于从后pop、从前push的队列背包。
两者形成了一个双端队列背包。
于是在DFS这棵版本树的过程中,维护双端队列背包,询问时直接给出答案即可。
由上一节的结论,总复杂度是$O(qP)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
|
int Main()
{
int q;
read(q);
std::vector adj(q + 1, std::vector<int>{});
std::vector last(q + 1, 0);
int n = 1, m = 1;
last[1] = 1;
std::vector upd(q + 1, std::array<int, 2>{});
std::vector qry(q + 1, std::vector<std::array<int, 2>>{});
int cnt = 0;
while (q--)
{
int op;
read(op);
if (op == 1)
{
int x;
read(x);
m++;
last[m] = last[x];
}
if (op == 2)
{
int x, p, t;
read(x, p, t);
int u = last[x];
int v = ++n;
adj[u].push_back(v);
last[x] = v;
upd[v] = {p, t};
}
if (op == 3)
{
int x;
read(x);
int u = last[x];
int v = ++n;
adj[u].push_back(v);
last[x] = v;
upd[v] = {-1, -1};
}
if (op == 4)
{
int x, p;
read(x, p);
cnt++;
qry[last[x]].push_back({p, cnt});
}
}
const int P = 2000;
std::vector dpL(1, std::vector<int>(P + 1));
std::vector dpR(1, std::vector<int>(P + 1));
std::deque<std::array<int, 2>> dq{};
std::vector<int> ans(cnt + 1);
auto DP = [&](std::vector<int> &pre, int p, int t) -> std::vector<int>
{
std::vector<int> dp(P + 1);
for (int v = 0; v <= P; ++v)
{
dp[v] = pre[v];
if (v >= p)
dp[v] = std::max(dp[v], pre[v - p] + t);
}
return dp;
};
auto rebuild = [&]()
{
int size = dq.size();
int l = size / 2, r = size - l;
dpL.assign(l + 1, std::vector<int>(P + 1));
dpR.assign(r + 1, std::vector<int>(P + 1));
for (int i = 1; i <= r; ++i)
{
auto [p, t] = dq[l + i - 1];
dpR[i] = DP(dpR[i - 1], p, t);
}
for (int i = 1; i <= l; ++i)
{
auto [p, t] = dq[l - i];
dpL[i] = DP(dpL[i - 1], p, t);
}
};
auto query = [&](int V, int i)
{
auto &dp0 = dpL.back();
auto &dp1 = dpR.back();
int res = 0;
for (int i = 0; i <= V; ++i)
res = std::max(res, dp0[i] + dp1[V - i]);
ans[i] = res;
};
auto pop_front = [&]()
{
dq.pop_front();
if (dpL.size() == 1)
rebuild();
else
dpL.pop_back();
};
auto push_front = [&](int p, int t)
{
dq.push_front({p, t});
auto dp = DP(dpL.back(), p, t);
dpL.push_back(dp);
};
auto pop_back = [&]()
{
dq.pop_back();
if (dpR.size() == 1)
rebuild();
else
dpR.pop_back();
};
auto push_back = [&](int p, int t)
{
dq.push_back({p, t});
auto dp = DP(dpR.back(), p, t);
dpR.push_back(dp);
};
auto dfs = [&](this auto &&self, int u) -> void
{
auto [p, t] = upd[u];
if (p < 0)
{
std::tie(p, t) = dq.front();
p = -p;
pop_front();
}
else if (p > 0)
push_back(p, t);
for (auto [V, i] : qry[u])
query(V, i);
for (int v : adj[u])
self(v);
if (p < 0)
{
push_front(-p, t);
}
else if (p > 0)
pop_back();
};
dfs(1);
for (int i = 1; i <= cnt; ++i)
printf("%d\n", ans[i]);
return 0;
}
|


